알고리즘
[백준/Python] 2839 설탕배달 | DP(다이나믹 프로그래밍)
파프리카_
2022. 3. 31. 21:15
728x90
반응형
📒 문제
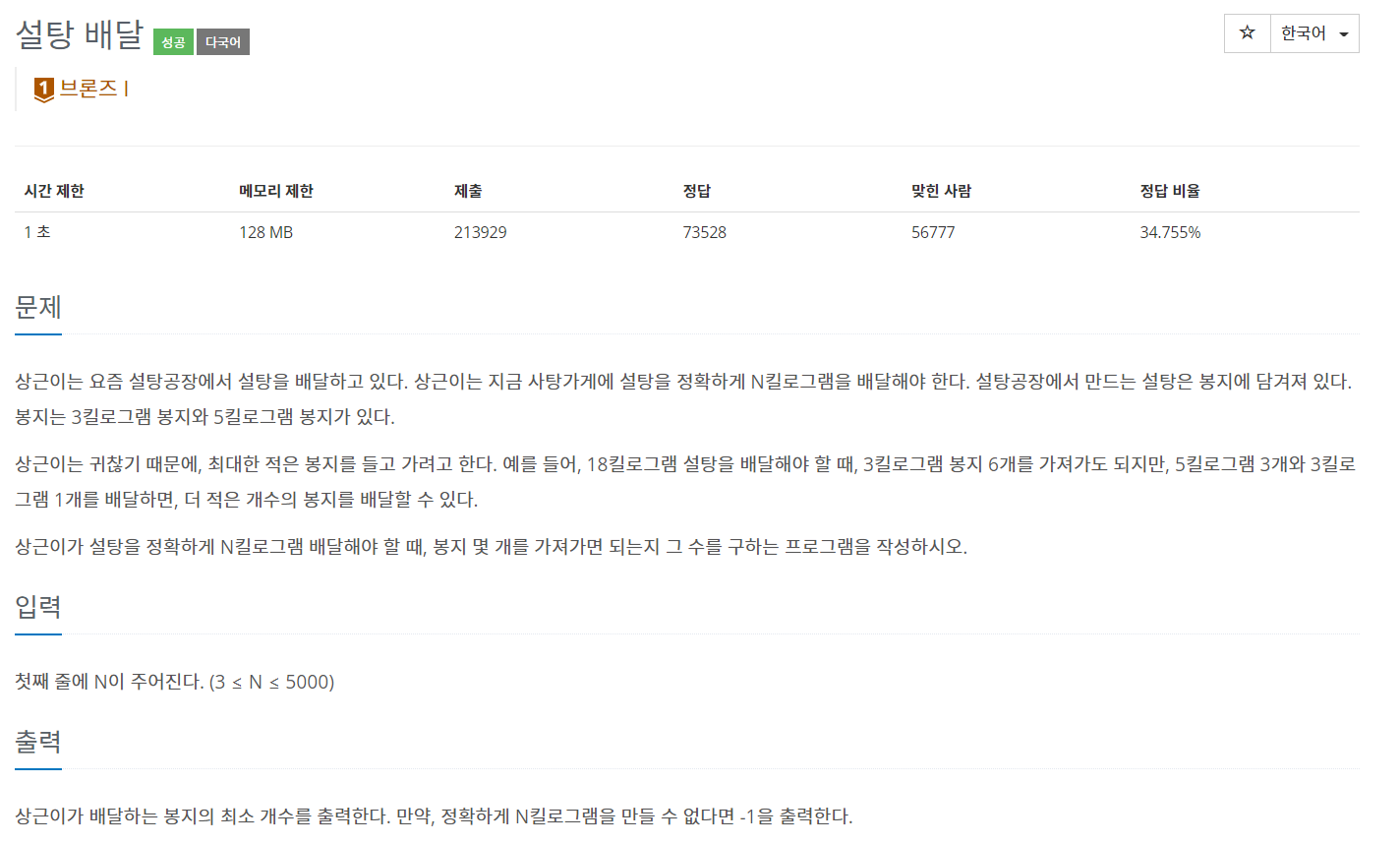
🤸♀️ 문제 분석
다른 블로그를 보면 반복문(while)로 구현하여 greedy 방법으로 푼 풀이가 많은데,
요즘 DP 연습을 하고 있기 때문에 DP로 접근하여 문제를 풀었다.
DP 테이블에는 '각 무게 별 사용하는 봉지의 최소값'을 저장한다.
이것을 가능하게 하는 조건은 아래와 같다.
3키로와 5키로 각각의 설탕봉지가 있기 때문에, 3키로 전 / 5키로 전 dp값에서 작은 값에 +1 한 값을 현재 dp에 할당하면 된다.
💡 경우의 수는 아래와 같이 세 가지 경우가 있다.
case 1) 3kg전, 5kg전의 봉지사용 최소값이 둘 다 존재하는 경우(봉지로 옮길 수 있는 경우), 두 값에 +1 한 것 중 작은 값을 현재 dp에 할당한다.
case 2) 3kg전 혹은 5kg 전 둘 중 하나만 존재하는 경우, 존재하는 값에 +1한 값을 현재 dp에 할당한다.
case 3) 3kg 전, 5kg 전 둘 다 최소값이 존재하지 않는 경우, 현재 값에서도 3kg, 5kg봉지로 옮길 수 없기에 이 경우에는 할당하지 않는다.
단, 5키로 이하의 값은 dp로 계산하지 않고, 해당 값의 dp에 미리 할당해준 값을 출력한다.
🧮코드
# 배달해야하는 설탕의 kg
n = int(input())
# dp : nkg에서 사용하는 봉지의 최솟값
dp = [-1 for _ in range(5001)] # -1로 초기화
# 3과 5는 각각 한봉지씩 들수있기때문에 1로 초기화
dp[3] = 1
dp[5] = 1
# 5이하일때는 dp하지 않고, 현재 값 출력
if n <= 5:
print(dp[n])
# dp 시작
else:
# 6 이상부터 n까지 dp확인
for i in range(6, n + 1):
# a : 5키로 추가 전 무게의 봉투 최소값
# b :3키로 추가 전 무게의 봉투 최소값
a, b = dp[i], dp[i]
# 현재 무게에서 5키로 추가 전 dp가 가능하다면 해당 값 할당
if dp[i - 5] != -1:
a = dp[i - 5]
# 현재 무게에서 3키로 추가 전 dp가 가능하다면 해당 값 할당
if dp[i - 3] != -1:
b = dp[i - 3]
# 3, 5키로 둘 다 가능하다면 둘 중 작은 값 선택
if a > 0 and b > 0:
dp[i] = min(a + 1, b + 1)
# 5키로 추가만 가능하다면 5키로 전 dp값에 1추가
elif a > 0 and b < 0:
dp[i] = a + 1
# 3키로 추가만 가능하다면 3키로 전 dp값에 1 추가
elif a < 0 and b > 0:
dp[i] = b + 1
# 둘 다 불가능하다면 연산 불가 (-1) 할당
else:
dp[i] = -1
# 현재 무게에서의 최솟값 출력
print(dp[n])728x90
반응형