📒 문제


🤸♀️ 문제 분석
연속 세 개의 계단을 이동할 수 없다는 것은 한칸->한칸 이동이 불가능 하다는 것이다.
1) 두칸 이동
2) 두칸 이동 후, 한칸의 이동만 가능하다.
정리하자면,
i 번째 계단에 오기 위해서는
1) i-2번째 계단(두칸전) -> i 번째 계단
2) i-3번째 계단(세칸전) -> i-1번째 계단(한칸전) -> i 번째 계단
둘 중 하나이다.
그림 설명!!!!
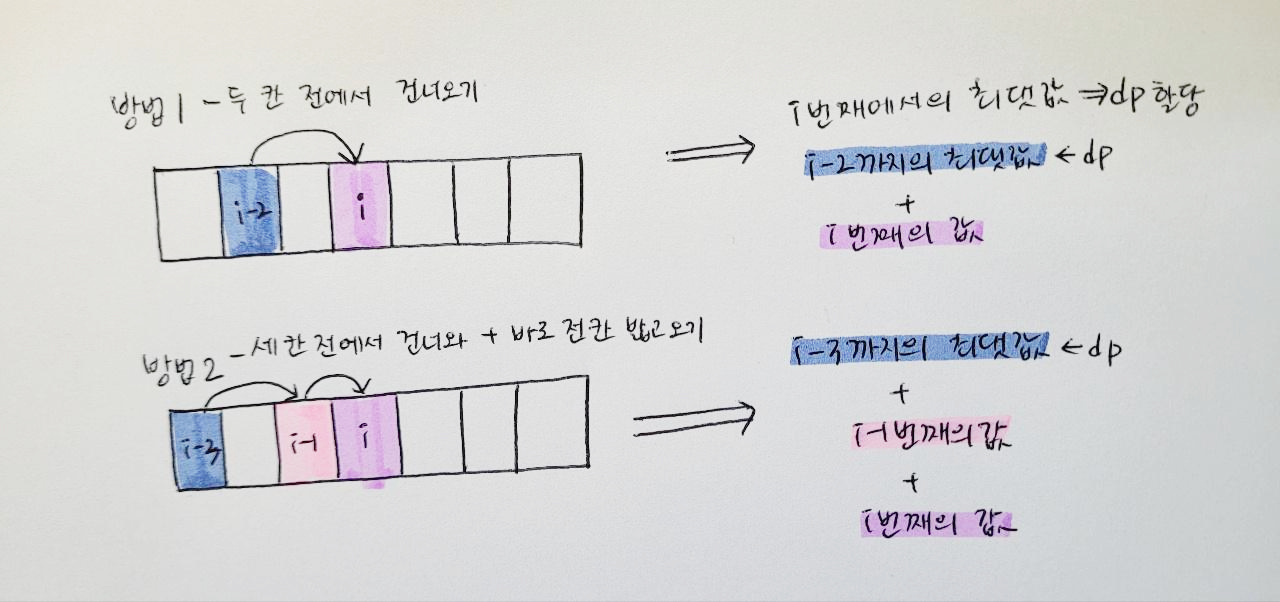
나는 방법1은 나름 납득이 되었는데,
방법2에서 i-3은 dp에서 i-3까지의 최대값을 가져오고, i-1번째는 그냥 배열의 값을 가져와서 더해주는 게 이해가 안됐다.
그냥 i-1번째까지의 최대값을 가져오면 되는 것이 아닌가! 싶었는데
i-1번째까지의 최댓값만 구하면 계속 한칸씩만 이동할 것이고 그렇다면 세 칸의 계단을 연속으로 가면 안된다는 조건에 위배된다.
그러므로 두 칸 전에서 건너올때는 두 칸 전까지의 최댓값(그 전에 한칸 이동했든, 두 칸 이동했든 일단 두 칸 전까지의 최댓값)과
한 칸 전에서 건너올 때는 반드시 그 전에 두 칸을 건너와야하는 규약이 있기에,
한 칸 전 + (한 칸의 두 칸 전인) 세 칸 전까지의 최댓값(이 역시, 세 칸 전까지는 한칸이든 두칸이든 규약을 주지 않고 그냥 최댓값이면 된다)을 비교하면 된다.
👩💻
소스코드로 구현하면,
dp의 초기값 할당은
- 첫번째는 첫번째 계단의 값
- 두번째는 첫번째 계단의 값 + 두번째 계단의 값 (두번째 계단까지의 최댓값은 무조건 첫번째를 들려오는 것이 크기때문에)
이렇게 할당해준다. (나머지는 그냥 0으로 했다)
그리고 세번째 계단부터 dp를 시작하며,
- 첫번째 계단(두칸이동) -> 세번째 계단
- 바닥(두칸이동)-> 두번째 계단(한칸이동) -> 세번째 계단
둘 중 큰 값을 세번째 dp의 최대값으로 할당해주면 된다.
이 때 바닥의 dp값이 필요하기에 dp의 0번째는 0으로 할당한다.
계단 배열도 dp와 인덱스를 맞추려면 배열 맨 앞에 0을 할당해주는 것이 편하다.
💡
그리고 혹시 계단이 한 칸인 경우를 대비해서,
코드 상에 계단이 한 칸만 주어지면 해당 값을 바로 출력해주어야 런타임에러로부터 자유로울수있다.
🧮코드
# n : 계단의 개수
n = int(input())
# 각 계단의 점수
steps = [0] # 시작점은 0으로 초기화
steps += [int(input()) for _ in range(n)]
# 각 계단에서의 최댓값
dp = [0 for _ in range(n + 1)]
def solution():
if n == 1:
return steps[1]
# 두번째 계단까지의 최댓값은 한칸씩 오른 값이다
dp[1] = steps[1]
dp[2] = steps[1] + steps[2]
# 세번째 계단부터 확인
for i in range(3, n + 1):
# 현재 계단에서의 최대값 구하기
dp[i] = max(dp[i - 2] + steps[i], dp[i - 3] + steps[i - 1] + steps[i])
return dp[n]
print(solution())'알고리즘' 카테고리의 다른 글
| [백준/Python] 2839 설탕배달 | DP(다이나믹 프로그래밍) (3) | 2022.03.31 |
|---|---|
| [백준/Python] 1901 회의실 배정 | 그리디(greedy) (0) | 2022.03.28 |
| [백준/Python] 11047 동전0 | 그리디(greedy) (0) | 2022.03.28 |
| python | 1439번. 뒤집기 | greedy(그리디) (0) | 2022.03.24 |
| python | 모험가길드 | 그리디(greedy) (0) | 2022.03.23 |



